Stupid Formulæ

I get annoyed by the stupid formulæ used by PR companies to generate nonsense ‘news’ reports about their clients’ products. I’ve done a talk about them at a couple of Skeptics in the Pub events, as well as Barcamps and the like. Email me if you’d like me to do the talk for you. (I’m pretty good.) Here is an adapted version of that talk for the web:

How to beat Blue Monday

So, another Blue Monday is upon us. It’s not clear exactly when Blue Monday is, but we do know it’s upon us. The Daily Mail has gone with last Monday; The Training Room, one of the four billion companies who have used it for marketing, have gone with next Monday. But we can work it out, because we have the equation:

…unless it’s this one:

but nobody uses that one. Anyway, it’s definitely a Monday, and it’s definitely in January because $T$ is time, which increases with time and so is highest in December, and $Q$ is how many new year’s resolutions you’ve given up on which is also highest in December look don’t think about it shut up.

Anyway, we know these formulæ are real because they make predictions. One intrepid PR man compiled a formula for the perfect marriage which results in thirty-some pre-specified romantic gestures you have to make every month. Since months are of different lengths, that means you need be less romantic in the longer ones.

Romantic Gestures Per Month
A Misleading Chart

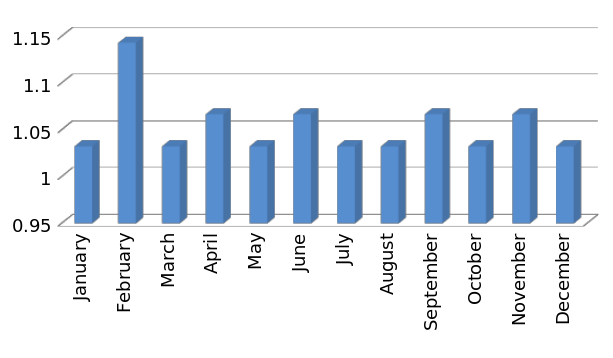
This formula about a marriage clearly makes the unrelated prediction that February should be the most romantic month; that there should be some kind of festival of romance smack in the middle of it. Since every restaurant I’ve been in lately has taken great pains to confirm that this is indeed the case, the only rational, skeptical or scientific conclusion is that these formulæ represent the very real cutting edge of science.

While it is obviously bad news that we are all scientifically depressed either last or next Monday, it does offer a ray of hope. Here, you see, is the formula for the perfect Christmas:

I’m assuming that the second “divided by 3D” on the bottom is a typo. Firstly because this formula otherwise defines some kind of festive acceleration, which even a cursory analysis of the Twelve Days Of Christmas song teaches us is dangerous, but mostly because if it’s a real fraction then the numerator has an equals in it.

The point of this equation is—

Actually, first I should point out that $W$ appears twice: once to represent a walk, and once to represent a glass of wine. This might be an error, but I prefer to assume it is a deliberate simplification introduced because walking and wine are somehow equal. I say this because this is the Times’ “Offset Your Carbs” wallchart:

It quite clearly shows that going for a walk is equal to garlic bread:

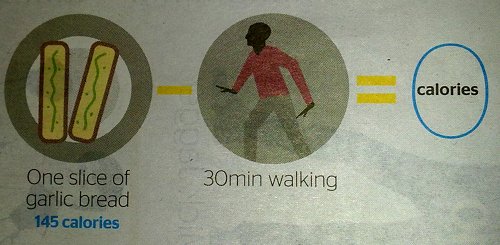
It also shows (although I haven’t got a close-up photo of this) that a glass of wine is equal to some sex. Taking the new result that wine equals walking,

The strangest thing here is that mathematically, Peter Kay is now the filthiest comedian in Britain.

Anyway, the point is that the $D$ in the formula for misery is Christmas debt. If we can reduce that value we can all-but eliminate Blue Monday. So how do we do that? Well, the formula for the perfect Christmas is:

Christmas debt is $8F \times 4P \times £23 = £736$. Quite a whack. But we can reduce it without affecting $P_\chi$ — I’m generously assuming what is probably an $X$ is a $\chi$ — because it’s in a fraction. Dividing top and bottom by 4, we get

That gets us below £50, but that’s still a lot. Let’s dispense with seven family members and divide through by eight.

Now our only problem is that the times are inconsistent: 135 minutes in the first term, and three days thereafter. Never mind, just divide all the fractions by 32, top and bottom:

This new, abbreviated Christmas is interesting. $G$, for example, represents a nice family game, of which we must play three thirty-second fractions, and while the formula for the perfect family game (obviously there is one) doesn’t readily divide by 32, there is a game that does.

Three Chess Over Thirty Two features six squares with three pieces on them, and luckily for anyone wanting to knock out Christmas in a little over two hours, requires only one move for checkmate.

But however dull a game Three Chess Over Thirty Two can be, however unsatisfactory one sixteenth of a glass of wine (or walk), and however overfilling you find the 32 portions of nut roast you are forced to consume because it was inexplicably on the denominator, the cold, mathematical reality is that $P_\chi$ has not changed and therefore Christmas has been totally and objectively perfect, while costing less than six pounds. This, in turn, means that our formula for misery loses much of its sting, and that is how you beat Blue Monday.